Prefix Sum

1. 구간 합 VS 부분 합

• Prefix sum(구간 합) : 구간 합이란 수들의 나열에서 특정 구간의 합을 의미한다. 구간 합 알고리즘은 보통 1차원배열에서 i~k 인덱스 사이의 값들의 합을 구하는데 사용한다.
• Partial sum(부분 합) : 부분 합이란 구간 합과 달리 처음부터 특정인덱스까지의 합을 의미한다. 즉 0~k 인덱스 사이의 값들의 합을 의미한다.

2. 구간 합 알고리즘

• 반복문을 사용하여 i~k사이의 값을 더하는 알고리즘의 시간복잡도는 O(n)이다.
• 이 같은 알고리즘을 사용할 경우 n의 값이 클 경우 이를 정해진 시간 내에 해결할 수 없다.
• 하지만 구간 합 알고리즘을 사용하여 구간합을 구하는 경우 O(1)의 성능을 갖는다.
• 구간 합 알고리즘은 현재 진행단계까지의 인덱스까지 값의 합을 저장하는 sum[]배열을 사용한다.
• j번째 바로 앞까지의 총합에 arr[j] 값을 더하면 j번째까지의 총합을 의미하므로 sum[j] = sum[j-1] + arr[j] 로 표현할 수 있다.

⇒ 포인트는 memoization 인듯

 

1차원 배열

arr을 순차 탐색하면서 sum 배열을 만들어주면 된다.

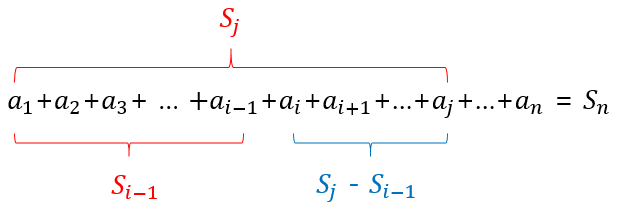
2차원 배열

2차원 배열도 같은 방식이다.  arr을 순차 탐색하면서, sum배열을 만들어주면 된다.

Sum[i][j]는 arr[0][0]부터 arr[i-1][j-1]까지의 합이다.

sum 배열 만드는 공식

sumArray[i][j]=arr[i-1][j-1]+sumArray[i-1][j]+sumArray[i][j-1]-sumArray[i-1][j-1]

 

 

 

 

2차원 누적합 구하는 문제 풀때 꼭 한번 읽어봐야할 글

https://nahwasa.com/entry/%EB%88%84%EC%A0%81-%ED%95%A9prefix-sum-2%EC%B0%A8%EC%9B%90-%EB%88%84%EC%A0%81%ED%95%A9prefix-sum-of-matrix-with-java#2%EC%B0%A8%EC%9B%90_%EB%88%84%EC%A0%81_%ED%95%A9_(prefix_sum_of_matrix) 

누적 합(prefix sum), 2차원 누적합(prefix sum of matrix) with java

 

 

 

그 외 참고자료

https://hroad.tistory.com/52

[알고리즘] 구간 합 (Prefix Sum)

https://san-tiger.tistory.com/entry/Prefix-sum-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EC%9D%B4%EB%9E%80

[알고리즘]Prefix sum 알고리즘이란?